The Rain Check
In this work, we check whether a deep learning model that does rainfall
prediction using a variety of sensor readings behaves reasonably. Unlike
traditional numerical weather prediction models that encode the physics of
rainfall, our model relies purely on data and deep learning.
Can we trust the model? Or should we take a rain check?
We perform three types of analysis. First, we perform a one-at-a-time
sensitivity analysis to understand properties of the input features. Holding
all the other features fixed, we vary a single feature from its minimum to
its maximum value and check whether the predicted rainfall obeys conventional
intuition (e.g. more lightning implies more rainfall).
Second, for specific prediction at a certain location, we use an existing
feature attribution technique to identify features (sensor readings by
location) influential on the prediction. Again, we check whether the feature
importances match conventional wisdom. (e.g. is ‘instant reflectivity’, a
measure of the current rainfall more influential than say surface
temperature).
Third, we identify feature influence on the error of the model. This is
perhaps a novel contribution; the literature on feature attribution typically
analyzes prediction attributions. Prediction attributions cannot tell us
which features help or hurt the accuracy of a prediction on a single sample,
or even globally. In contrast, error attributions give us this information,
and can help us select or prune features.
The model we chose to analyze is not the state of the art. It is flawed in
several ways, and therefore makes for an interesting analysis target. We find
several interesting issues. However, we should clarify that our analysis is
not an indictment of machine learning approaches; indeed we know of better
models ourselves. But our goal is to demonstrate the applicability of our
interactive analysis technique.
The Task
The task is to produce a nowcast, i.e., a prediction of rainfall a few hours
into the future. The input to the model are atmospheric and surface
observations from NOAA’s High-resolution Rapid
Refreshhttps://rapidrefresh.noaa.gov/hrrr/ dataset. We use
fifty six
featureshttps://rapidrefresh.noaa.gov/hrrr/HRRRv4_GRIB2_WRFTWO.txt
such as temperature, humidity, cloud cover, etc.. The target of our nowcast
is gauge corrected
MRMShttps://vlab.noaa.gov/web/wdtd/-/qpe-w-gauge-bias-correction
that provides 1 hour accumulated precipitation rates in millimeters. The inputs and the
outputs are both defined over a geospatial grid with a resolution of one
square kilometer. The entire dataset is collected over Continental United States.
Deep Learning vs. Numerical Weather Prediction
In this work, we analyze the predictions of a deep learning (neural
network) model. These models operate differently from traditional numerical
weather prediction (NWP) models. NWP models use the same data as input, but
rely on hand-engineered structured equations that encode the physics of
rainfall. In contrast, the deep learning models learn a function from
inputs to predictions without additional inductive bias (i.e., feature
design). While the DL approaches are data-driven, i.e., they learn from
patterns in the observations that are not directly encoded by physics, they
have been successful at certain weather prediction tasks . An advantage is that it is computationally efficient; producing a single prediction takes a second or less, whereas the NWP model needs to solve a large system of differential equations and could take hours to produce a single prediction.
The drawback of pure deep learning approaches is that we do not constrain
the model to respect the laws of physics, and therefore there is a risk
that deep learning models could rely on a non-causal correlation. We seek
to confirm that our deep learning model behaves consistent with our
knowledge of physics, and is trustworthy.
The Model
We analyze a rainfall prediction model that produces a forecast of the
quantity of rainfall (measured in mm/hr over a 1kmX1km area) three hours
into the future. The model takes 56 atmospheric and surface observations at
time \(t_0\) as input, each of which is a gridded \(256 \times 256\) image.
As a standard practice, we normalize all the features to be in the
range\([0, 1]\). The label (ground truth) is a \(256 \times 256\) gridded
map representing the actual rainfall three hours into the future.
The model is a neural network using an architecture called residual U-Net
consisting of convolution, upsampling, downsampling and ReLU activations.
We use a ReLU in the final layer to constrain the model to predict
non-negative rainfall. The model is trained using mean squared error as the
loss function. The model is also L2 regularized. We refer the reader to
Agrawal et al for more details about the architecture.
The model has an L2 (mean squared error) of 0.905. Contrast this with
HRRR, a numerical weather prediction model, that has an L2 of 5.181. This
difference in performance could stem from multiple sources: (a) The HRRR
model is not tuned for L2 loss. (b) The HRRR model takes longer to produce
a forecast, and therefore must rely on older data because it needs a longer
gap between the instant at which sensor readings are collected and the
instant of the forecast.
Here we show a few predictions of the model. On the left is the
actual rainfall (groundtruth/label), in the middle is the
prediction made by the model, and on the right is the mean
squared error.
One-at-a-time Sensitivity Analysis
In this section, we study the model's sensitivity to input features using
the one-at-a-time analysis (OAAT). In an OAAT analysis, we vary a single
feature (e.g. changing from low pressure to high pressure) holding all the
other features fixed, and note the change in the rainfall prediction along
this variation path. We then check whether the variation is as expected.
Sparsity in the data, or lack of regularization can make a model fail the
conditions that we know to be true from the physics of rainfall. We perform
the analysis for our model, and also a variant without L2 regularization.
Method: For each sample, and for each feature, holding all other
features constant, we vary the feature (all 256 X 256 values of the
feature) from its minimum value (0 due to normalization) to its maximum
value (1 due to normalization). We aggregate the results across the 1000
samples and produce a plot. The y-axis is the average prediction per pixel
in mm/hr.
One-at-a-time sensitivity analysis plot for all 56 features.
The x-axis is the step from 0 to 1 and the y-axis is the
average prediction per pixel in mm/hr.
Learnings
-
We find that the model's prediction is monotonically increasing for
features such as radar reflectivity (refc, refd-1000),temperature
(temp), relative humidity (r). Radar reflectivity measures the current
rainfall, three hours before the forecast, at various heights. These
results are all as expected. as higher reflectance implies higher
precipitation rate and similarly for humidity. Hotter temperatures
imply lower pressure which in turn imlies increasing chance of
precipitation.
-
Similarly, the model's prediction is monotonically decreasing in
features such as pressure at cloud top, mean sea level pressure and
ground heat flux; again this is as expected.
-
Some features exhibit unexpected dependency plots. For instance, the
model predicts less rainfall as there is more lightning (see the plot
for atmosphere_instant_ltng) and it predicts low rainfall for low
convective inhibition (surface_instant_cin). Upon further analysis, we
found that data for the lighting and convective inhibition also follows
this pattern, i.e., samples where there is less lightning have a higher
average rainfall and where there is low convective inhibition there is
low rainfall, respectively. But this is because the data for these
features is sparse, and therefore the model is picking up on a spurious
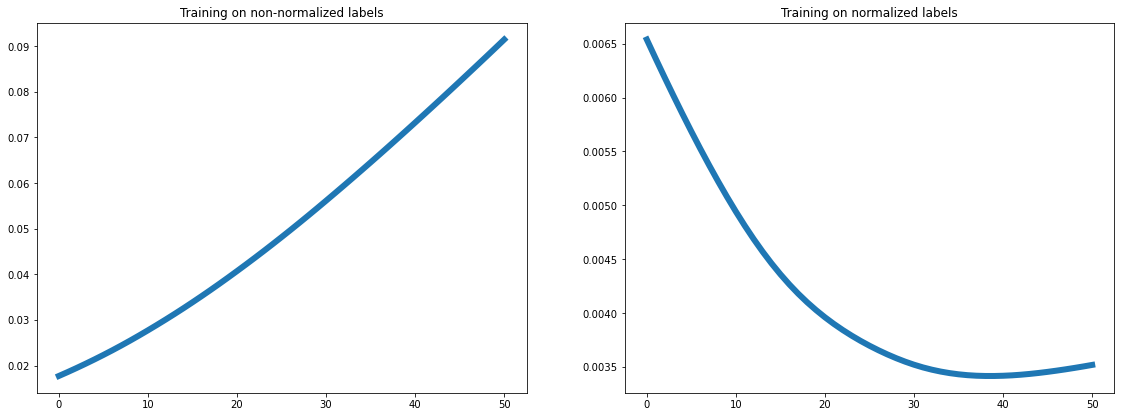
relationship. One way to correct the model for this feature was to
train the model on normalized labels, and on doing so convective
inhibition showed the expected dependency plot:
Feature Attributions
We use feature attributions to explain the behavior of the rainfall prediction model.
What is Feature Attribution?
A feature attribution technique attributes a machine learning model's
prediction to its input features; influential features get higher
attributions. Influence can either be positive (supporting the
prediction) or negative (opposing the prediction). Typically, the
prediction is a single scalar output, for instance for an object
recognition task (e.g Imagenethttps://image-net.org/), the prediction is a probability of the
image containing a specific object (e.g. a boat, or a tank, a specific
dog breed etc.). The attributions identify which pixels are most
influential to the prediction. In our case, there is a separate
prediction for every one of the 256X256 locations. In a later section we
discuss how to aggregate the attributions across locations; for now, let
us imagine we have to explain predictions for a single location.
Saliency Maps
Feature attributions are visualized using images called saliency
maps. Saliency maps have the same resolution as the input. For our
rainfall prediction task, we display a separate saliency map (across a
spatial grid) for every feature. On a saliency map, a pixel's shade
determines its importance. In our visualizations, shades range from green
for positive influence to purple for negative influence. The value of the
saliency map at a specific pixel says how much that feature at that
location contributed to rain in the selected output location(s).
Integrated Gradients
We use a feature attribution technique called Integrated Gradients. It has been used to explain
a variety of deep-learning models across computer-vision, NLP,
recommender systems, and other classification tasks.
Here is an informal description of Integrated Gradients. The technique
operates by perturbing features. Intuitively, perturbing an important
feature will change the score more substantially than perturbing an
unimportant feature; an infinitesimal perturbation is a gradient of the
score wrt the features. Integrated Gradients accumulates these gradients
along a path that results from linearly varying each feature from a
baseline value to actual input value. The baseline value for features
selected so as to force the prediction of the model to near zero. (We
discuss the selection of the baseline below). The score of the model
therefore varies along this path from zero to the actual output value.
Mathematically, the attribution to a single feature \(i\) is defined as:
$$ \phi (x_i) = (x_i - x_i') \int_{\alpha=0}^{1}
\frac{\delta F(x_{\alpha})}{\delta x_i} d\alpha \cdots (1)
$$
Here the input is \(x\), the baseline is \(x'\), \(F(x)\) is the output
of model, \(\frac{\delta F(x_{\alpha})}{\delta x_i}\) is the gradient of
\(F(x)\) along the \(i^{th}\) feature and \(x_{\alpha} = x' + \alpha
\times (x - x')\).
Integrated Gradients satisfies several desirable
properties, and in fact, uniquely so (see Corollary 4.4
here).
We highlight one such property called 'completeness'. Integrated
Gradients accounts for the change in the score from the baseline value to
the actual output value. This is a simple consequence of the fundamental
theorem of calculus; integrating derivatives (gradients for a
multivariable function) between two points \(x\), \(x'\) yields the difference
between the functions at the two points. That is, the sum of the
attributions over all the input features is equal to \(F(x) - F(x')\). Since
we select a baseline that sets \(F(x')\) to zero, the attributions can be
interpreted as a redistribution of the score.
Baseline Selection
As discussed, we select a baseline so as to minimize the prediction of
the model, i.e., set the predicted rainfall to zero. To do this, we
leverage our one-at-a-time analysis. If the rainfall prediction is
monotonically increasing in a feature, we set its baseline value to its
trimmed minimum value (1st percentile). If the function is monotonically
decreasing, we set the baseline value to the trimmed maximum value (99th
percentile). The trimming is to ensure that our baselines aren't
sensitive to outliers. If the function is convex or concave, we set the
baseline at the single local minimum.
Using the described method we get a zero rainfall prediction.
Extending Integrated Gradients to Analyze Error
Feature attribution methods are typically used to study predictions. In
this section, we extend the approach to apply to the model's error/loss. To
the best of our knowledge, this is a novel application of feature
attribution.
We will identify features that have a positive influence (decrease error)
on the quality of the model's prediction on the input, versus those that
have a negative influence (increases error). This analysis requires
knowledge of the groundtruth, and can only be performed after it is
available (once the three hours have elapsed in our case.)
We derive the analytical form of feature attributions for error. Let \(E\)
denote the squared error of the model's prediction:
$$ E(x) = (L(x) - F(x))^2$$
here \(L(x)\) is the label of the input.
We integrate the gradient of the error along the linear path (defined by
the parameter \(\alpha\)) from the baseline \(x'\) to the input; here
\(x_{\alpha}\) is a point along the path. Throughout this process, we hold
the label fixed at its input value \(L(x)\); this quantity is the model's
target. The attributions reflect how the model makes progress towards
reducing (or increasing) error along this path.
The attribution for a feature \(i\) is:
$$ \phi (x_i) = (x_i - x_i') \int_{\alpha=0}^{1}
\frac{\delta (L(x) - F(x_{\alpha}))^2}{\delta x_i} d\alpha \cdots (2)
$$
$$ \phi (x_i) = (x_i - x_i') \int_{\alpha=0}^{1} 2(F(x_{\alpha}) - L(x))
\frac{\delta F(x_{\alpha})}{\delta x_i} d\alpha \cdots (3)
$$
The second step is via application of the chain rule: the gradient of the
function \(E\) with respect to a feature can be written as the gradient of the
function \(E\) with respect to the score \(F\) , which is \(2(F(x) - L)\) times the
gradient of the score wrt the feature \(\frac{\delta F(x_{\alpha})}{\delta
x_i}\)
Compare this to the expression in Equation 1. The difference from
prediction attributions is the scaling by the term \(F(x) - L\) which
changes the scale and sign of the gradients being accumulated.
Aggregating Attributions
Thus far, we have discussed how to identify influential features (with
localities) for a prediction at a single location in the grid. However,
this is not directly usable because as analysts/meteorologists, we would
prefer explanations for a groups of locations such as a locality where rain
is predicted everywhere, or a locality where the model is inaccurate, or on
the entire 256X256 output grid, to understand the aggregate influence of
individual features. It would be painful to communicate these explanations
pixel by pixel. Fortunately, the attributions are in prediction units
(i.e., in quantity of precipitation), therefore we can sum attributions for
a set of output pixels; the attribution for a feature, location combination
now corresponds to how much it contributes to the total rainfall in the
selected output pixels.
Using Rain Checker
You can inspect the prediction and error attributions and feature
importance using the tool below in the following ways:
- Use the dropdown menu at the top to analyze prediction or error
attributions.
- Select any of the first three images from the sample selector at
the bottom to analyze individual samples.
- Select the last image in the sample selector to analyze the
aggregate of attributions over 200 samples (global). We filtered
out examples with high rainfall (> 3.5 mm) from this set, because
we found that the model was severely underpredicting on these
instances.
- The tool by default reorders the features by importance of
increasing attributions or lowering loss. If you would like to study
the effect of a specific feature across locations or samples,
uncheck the box.
- Click around over the image in the second row to select different
segments to analyze. Each segment has 16X16 pixels.
- The 'Total segment attribution' score is a sum of prediction /
error of all pixels in the selected segment.
- The scores over attribution maps for each feature are a sum of
the attributions over all the pixels for that input feature.
- Hover over the input feature or its corresponding attribution map
to see a descriptive name for each feature.
Select any segment over the prediction to view the ranking of
different features based on their total attribution.
Learnings
- Some features consistently receive high attribution across samples
and locations, driving predictions and a reduction in error.
- Maximum Radar Reflectivity (refc) and Radar Reflectivity at
1000m above ground level (refd-1000) consistently ranks in the top 5
features. This is expected because it is a direct measure of the
rainfall (three hours before the prediction), and rainfall now is
likely to imply rainfall later.
- For low-medium rainfall regions \((>0.5mm/hr)\) cloud-top
pressure (ct-pres) and cloud-base pressure (cb-pres) are
consistently the top two input features. We know that tall, deep
clouds are likely to produce precipitation, and these two
features estimate the height and thickness of the cloud
https://www.goes-r.gov/products/baseline-cloud-top-pressure.html.
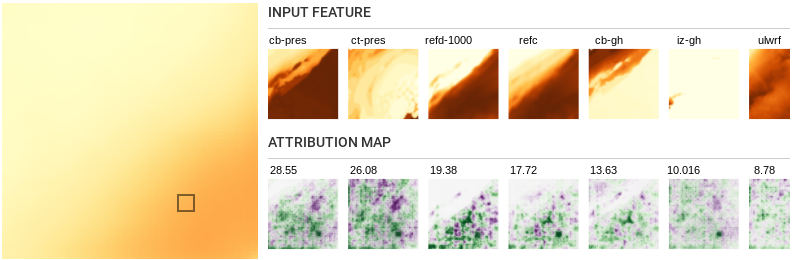
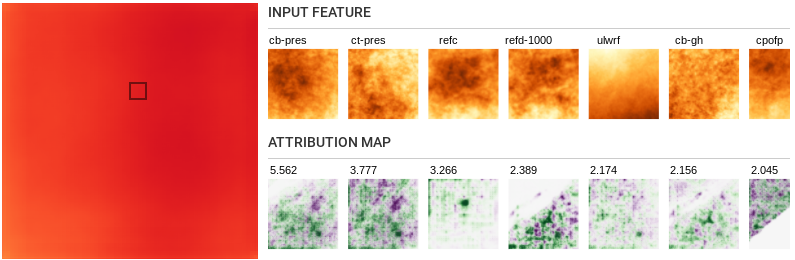
-
When examining the global attributions, for most segments, upward
longwave radiation flux (ulwrf) shows up as one of the top
important features. It measures the amount of thermal radiation
emitted by the Earth’s surface and clouds into the atmosphere.
Low amounts of ULWRF are considered representative of deep
convection and are used as a heuristic indicator of cloudiness
and precipitation estimation
.
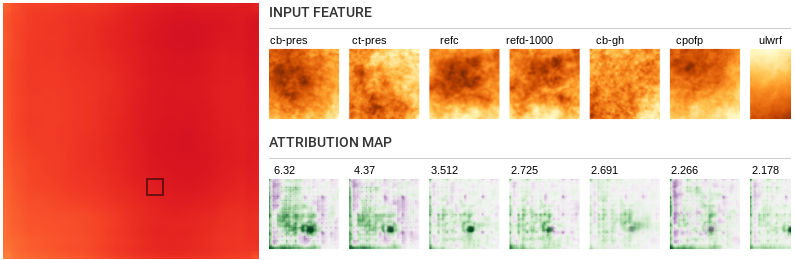
- Left to right influence:
- We see that output pixels are regularly influenced by feature
locations on the left of the pixel. This is likely due to the
Coriolis effect
https://en.wikipedia.org/wiki/Coriolis_force#Applied_to_the_Earth
that creates winds blowing from west to east
(Westerlies)https://en.wikipedia.org/wiki/Westerlies.
One obvious consequence of this is that the model will likely not
generalize to locations with different prevailing winds, say in
south Asia. This also suggests that care should be taken in
training models like this in regions with monsoonal circulation
patterns.
- Local influence:
-
For features like relative humidity (r) and total cloud cover
(tcc), the location in the input corresponding to the selected
output pixels has a positive influence on rain, however
surrounding regions have a negative influence on rain.
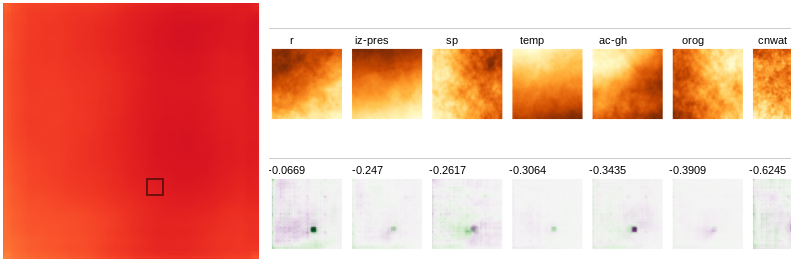
-
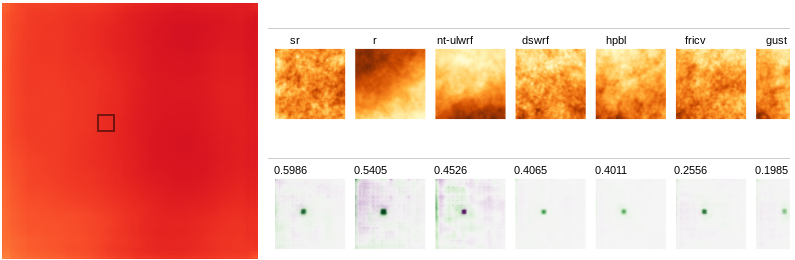
Features such as frictional velocity (fricv), surface lifted
index (lftx) and downward shortwave radiation flux seem to have a
strong influence from the same region as the chosen segment and
not much from other places around.
- Border artifacts:
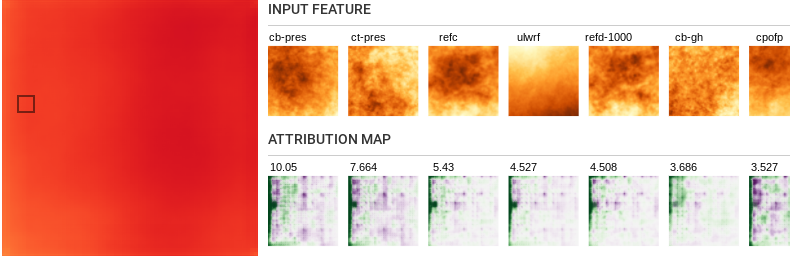
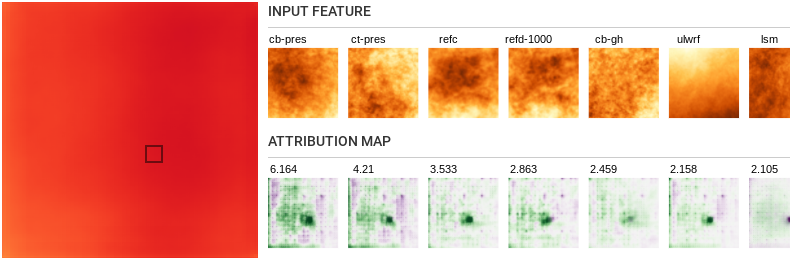
-
Notice that on analyzing segments close to the borders of the
sample, especially the left border, we see high attribution
values along the edges. This is however not the case for segments
closer to the middle of the sample. This clearly shows that
predictions at the border are weaker due to the lack of
information from spaces outside the sample. This could help trim
down our predictions to regions with high quality predictions.
Conclusion
We analyze a deep learning network that has superior accuracy in
forecasting rainfall three hours out than HRRR, a forecast system based on
traditional numerical weather prediction.
Our motivation was to check whether the deep learning model obeys causal
patterns indicated by the physics of rainfall. We found this to be largely
the case. The most influential features (pressure differentials, and
measures of current rainfall) were as expected. However, we did notice
breakages of causality as well. First, we found that the model predicted
less rainfall with more lightning, an issue possibly stemming from the
sparsity of data. Second, we found that rainfall predictions at a location
tended to depend on sensor readings towards the left. This is a consequence
of building a model on training data from the continental U.S., where the
prevailing wind direction is left to right. This indicates that the same
model wouldn't be suitable for predicting rainfall in other geographies.
Perhaps adding features such as wind direction and ground elevation could
produce a more causal model.
Finally, we expect our explainable, i.e., our feature attribution
exploration widget, to apply to the influence of features on predictions
and more importantly on the error/loss of the model, across a number of
weather tasks including wind, solar energy, flood and wildfire prediction,
that all share the characteristic of producing predictions across a spatial
grid.